树是一种分层数据结构的抽象模型。常见的例子是家谱,或公司的组织架构图。
树相关的术语
- 根节点
- 子树
- 树的高度
- 树的深度
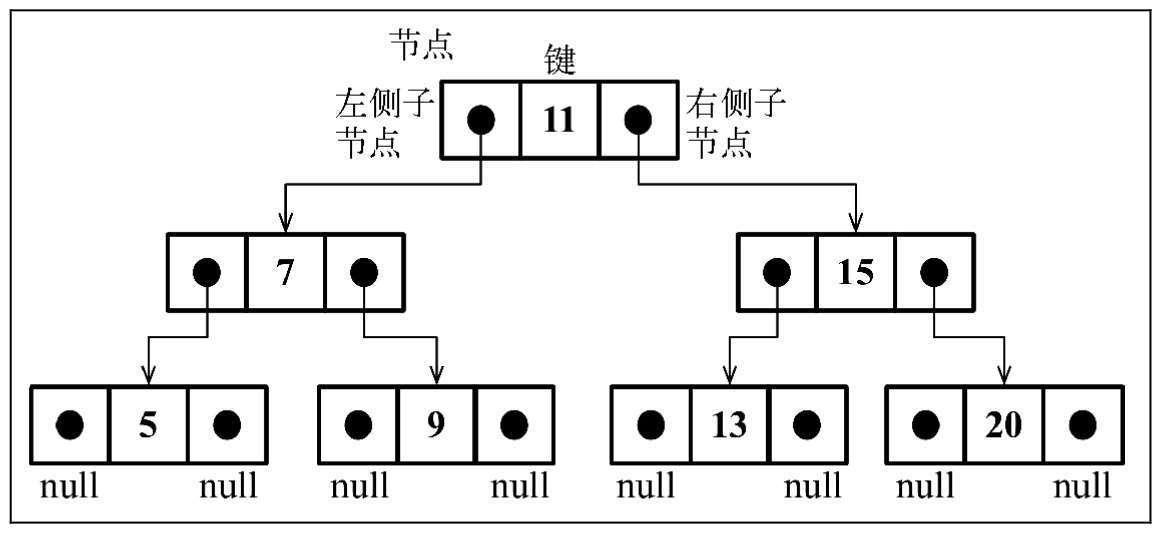
二叉搜索树
二叉树:节点只能有两个子节点。一个时左侧子节点,另一个时右侧子节点。
二叉搜索树(BST): 二叉树的一种,左节点小于父节点,右侧节点大于父节点。
BST各节点之间的排列形式总是如下
中
小 大
二叉树搜索树数据结构的组织方式
二叉搜索树的方法
insert(key)在树中插入一个新的键search(key)在查找节点preOrderTraverse()先序遍历所有节点inOrderTraverse()中序遍历所有节点postOrderTraverse()后序遍历所有节点min()返回树中最小的值/键max()返回树中最大的值/键remove(key)返回树中最小的值/键
树的遍历
- 先序遍历: 根左右
- 中序遍历: 根左右
- 后序遍历: 根左右
最小值:树的最后一层最左侧的节点
最大值:树的最后一层最右侧的节点
因此寻找最小值,总是沿着树的左边寻找;寻找最大值,总是沿着树的右边寻找
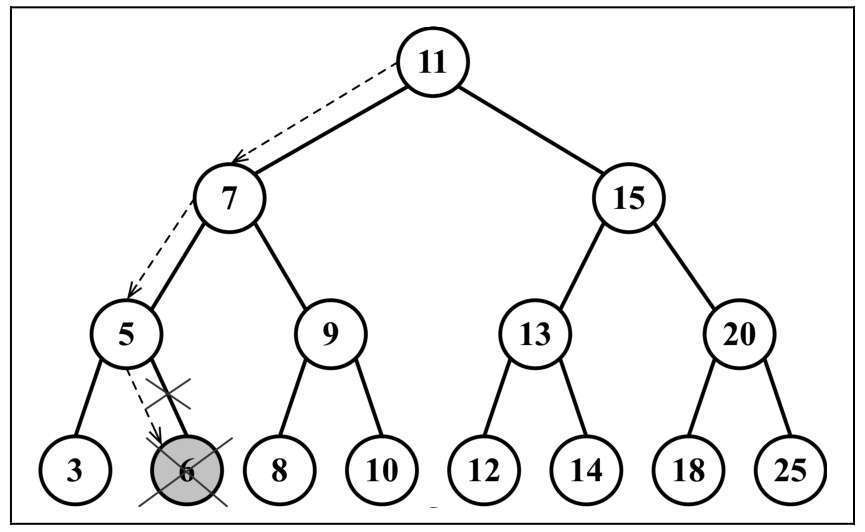
删除节点
移除叶子节点
移除
6即可
移除只有左侧子节点或只有右侧子节点的节点
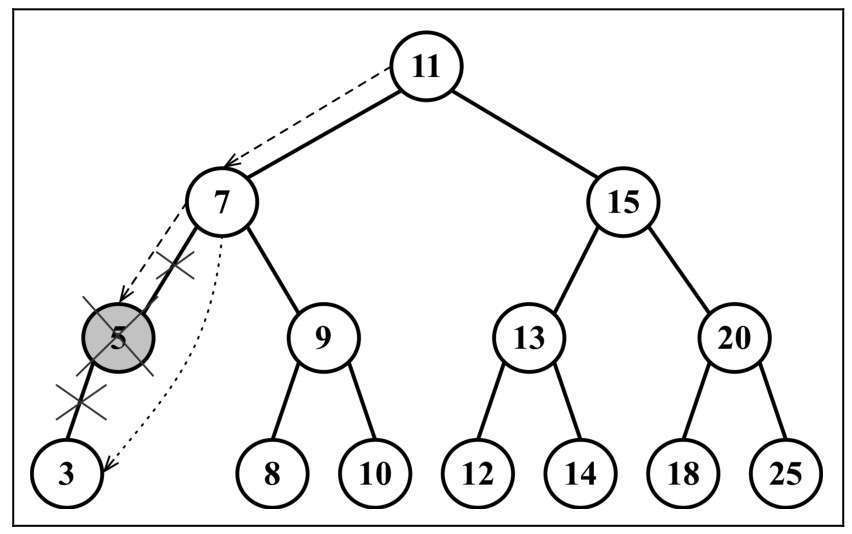
移除
5,把7的子节点修改为3
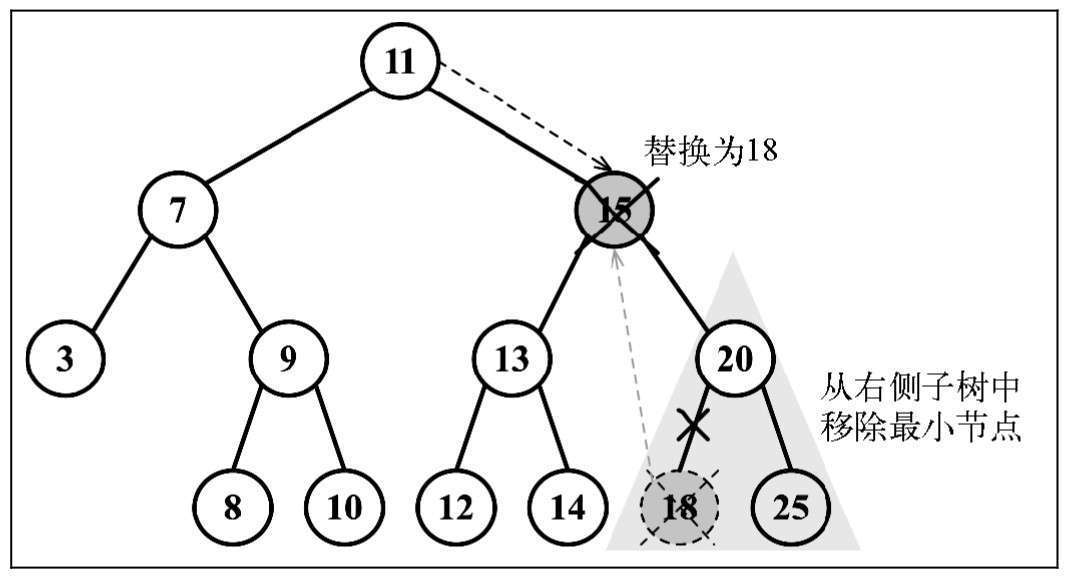
移除存在两个子节点的节点
移除
15,找到15节点的右子树最小的节点(即右子树左下角的节点)18填充15的位置,并删除原有的18
代码实现
自平衡树
自平衡树 AVL 在添加或移除节点时,会尝试保持自平衡,使任何一个节点左右两侧子树的高度之差为 1 。
平衡操作 —— AVL 旋转
左-左 (LL) 向左的单旋转 右-右 (RR) 向右的单旋转 左-右 (LR) 向右的双旋转(先LL旋转,再RR旋转) 右-左 (RL) 向左的双旋转(先RR旋转,再LL旋转)